・計算の種類

　　　計算には次の種類があり、それぞれオーダーがある。項のオーダーは、物理量、作用素、計算のオーダーの足し算で決まる。

　　・オーダー0の計算

　　　オーダー0の作用素には加算、減算、乗算などがある。

　　　・加算、乗算

　　　　　ベクトルの計算

　　　　　

　　　　　テンソルの計算

　　　　　

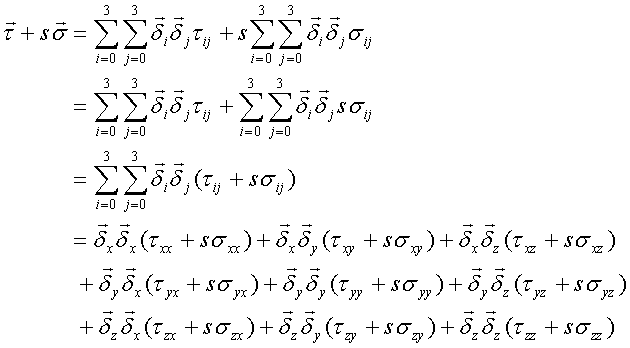
　　　　　減算も同様に計算できる。

　　　・微分作用素を含む場合

　　　　スカラーの微分

　　　　

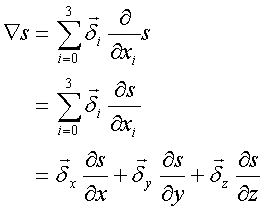
　　　　ベクトルの微分

　　　　

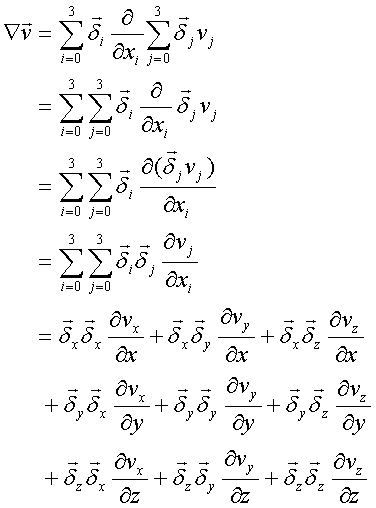
　　　　ベクトルのラプラシアン

　　　　

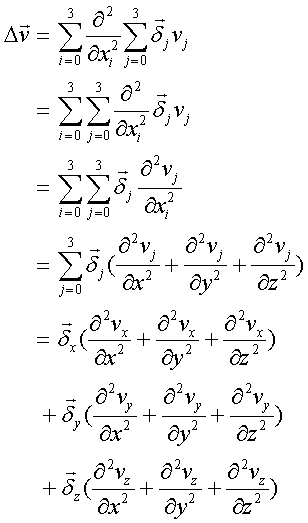
　　・オーダー-2の計算

　　　オーダー-2の計算には内積がある。

　　　計算の準備

　　　　・クロネッカーのd_ij

　　　　　ベクトル、テンソルの計算に使用する。

　　　　　　

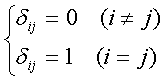
　　　　　内積計算はこの記号を用いて下記で定義される。

　　　　　　

　　　　　　

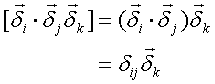
　　　　　これは、内積の定義から説明される。

　　　　　　

　　　　　　

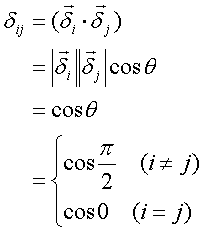
　　　　ベクトルとベクトルの内積

　　　　　

　　　　上記の項のオーダーは、

　　　　　(ベクトル・ベクトル) = (1 – 2 + 1) = 0

　　　　と計算されるので、スカラー量になる。

　　　　　

　　　　また、下記が成り立つ。

　　　　　

　　　　微分作用素とベクトルの内積

　　　　　

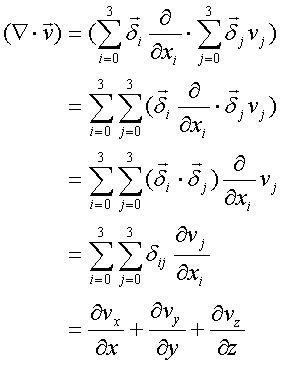
　　　　上記の項のオーダーは、

　　　　　(微分作用素・ベクトル) = (1 – 2 + 1) = 0

　　　　と計算されるので、スカラー量になる。この物理量は発散と呼ばれ、微小要素への流入・流出量を表している。

　　　　　　　

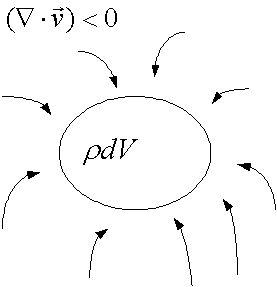
　　　　 → 微小要素へ物理量が流出した

　　　　 → 微小要素への流入・流出は無い

　　　　 → 微小要素へ物理量が流入した

　　　　上記からわかるように発散とはx, y, z軸方向の勾配の和であり、0の場合は、平らなので流入・流出は無いと解釈できる。

　　　　また、下記が成り立つ。

　　　　　

　　　　微分作用素とテンソルの内積

　　　　　

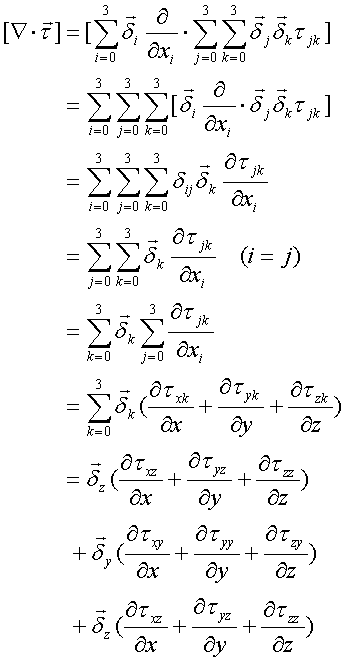
　　　　上記の項のオーダーは、

　　　　　(微分作用素・テンソル) = (1 – 2 + 2) = 1

　　　　と計算されるので、ベクトル量になる。

　　　　また、下記が成り立つ。

　　　　　

　　　　ラプラシアン作用素

　　　　ラプラシアン作用素は、微分作用素の内積で表される。

　　　　　

　　　　上記の項のオーダーは、

　　　　　(微分作用素・微分作用素) = (1 – 2 + 1) = 0

　　　　と計算されるので、スカラー量になる。

　　　　全微分作用素

　　　　流体力学で使用する全微分作用素には、内積が使用されている。

　　　　　

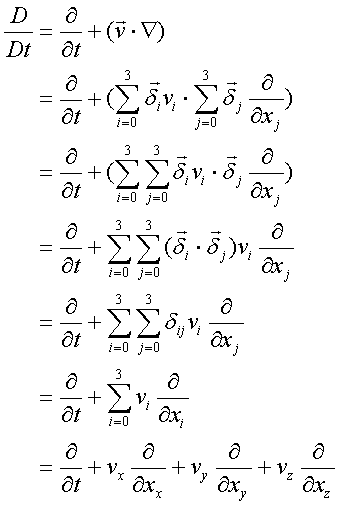
　　　　上記の項のオーダーは、

　　　　　(ベクトル・微分作用素) = (1 – 2 + 1) = 0

　　　　と計算されるので、スカラー量になる。

　　　　これは、流体力学で使用される。微小領域の変化量をテーラー展開した1次の項である。

　　　　内積から角度の計算

　　　　内積から2つのベクトルの角度が計算できる。

　　　　　

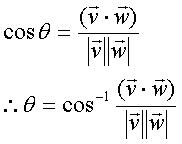
　　　　数値計算で要素の変形度や作成時に使用する。

　　・オーダー-1の計算

　　　オーダー-1の計算には外積がある。

　　　　準備

　　　　外積の計算には次の記号が用いられる。

　　　　　

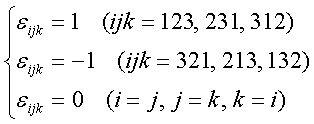
　　　　ベクトルとベクトルの外積

　　　　　

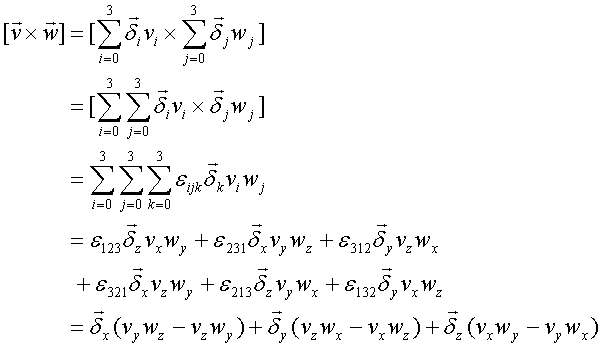
　　　　ベクトルとベクトルの外積の成分は、2つのベクトルで表される平行四辺形の面積を表している。次の様にも表される。

　　　　　

　　　　従って、2つのベクトルが平行の時は、外積は0になる。

　　　　　

　　　　微分作用素とベクトルの外積

　　　　　

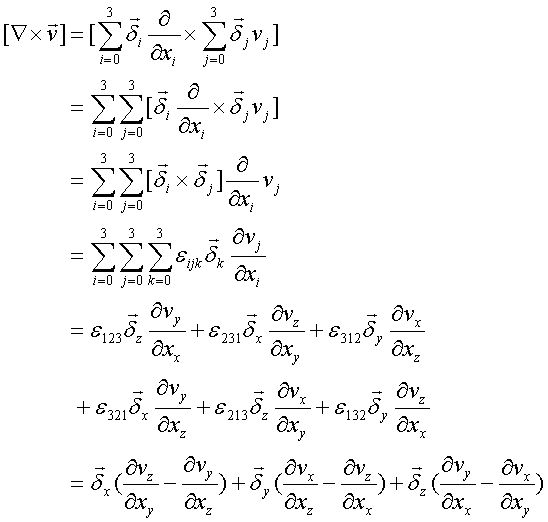
　　　　微分作用素とベクトルの外積は、渦度と呼ばれる。これは、台風や海の渦巻きの様に回転に対して垂直方向のベクトルを表している。回転方向のベクトルを用いて表される。

　　　　　

　　　　　

　　　　　

　　　　　

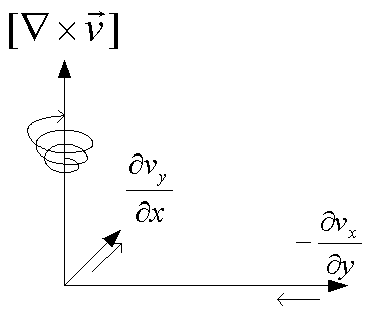
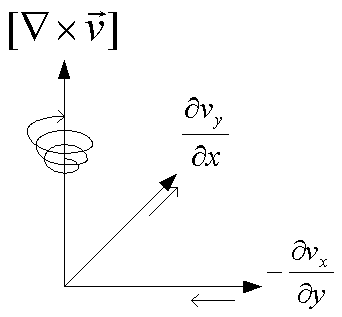
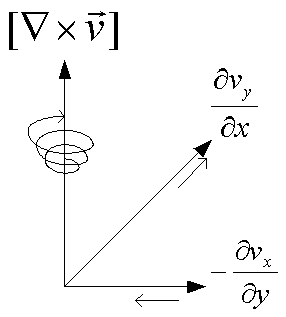
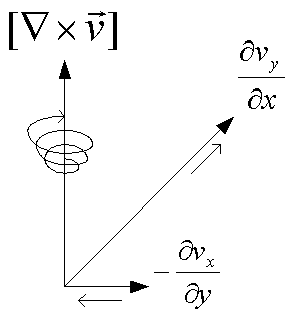
　　　　微小平面で考えると良くわかる。