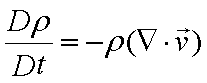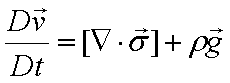広告
コラム:微分と積分
坂道を運転している時に「この道は勾配が急だなー」とか「ここは勾配が緩やかだよなー」 と言う表現をすることがある。勾配が急だとより短い距離で高い位置に行けるが、緩やかだと なかなかたどり着かない。要するに勾配とは変化の激しさを表している。
「この道は上がったり下がったり勾配が変りやすいなー」というのが勾配の勾配である。 流体力学では、基本的にこの勾配の勾配まで出てくる。「勾配の勾配の勾配」は出て来ない。 勾配とは、微分のことである。車が坂道を登る様子を断面図で見れば、まさにxy座標を表している。
「道はデコボコしていたが、最終的にこの高さまで到達した。」と言うのが積分である。 積分は結果であって過程は問われない。逆を言えば、結果の高さだけを言われても、 どういう道を辿ったかはわからないと言うのが積分である。
仮に、道の高さによって酸素の消費量が変るとして、 最終的な酸素消費量は幾らかを考える計算は、関数の積分である。 その時々の酸素消費量を計算して、細切れ全てを積算するとわかる。 細切れは、極限まで細かくされる。
| prev | | | top | | | next |