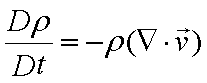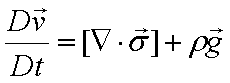広告
3角形1次要素
無次元化した熱収支式は次式となります。
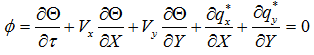
内挿関数Niを重み関数に使用すると離散化式は次式となります。
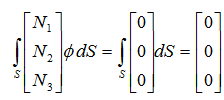
速度、温度は、内挿関数Niを用いてそれぞれ次式で表されます。
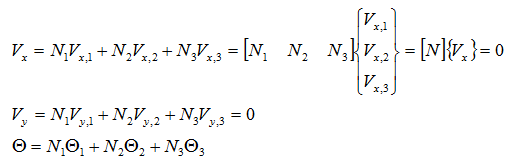
従って、離散化式は、次式となります。
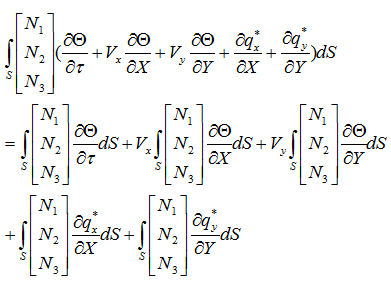
展開すると
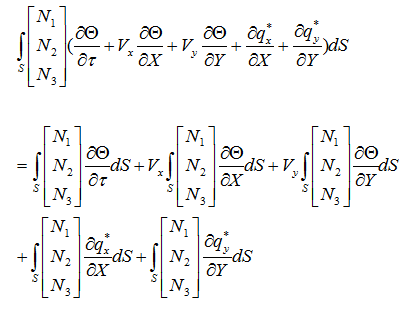
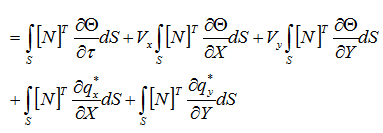
グリーン・ガウスの定理より
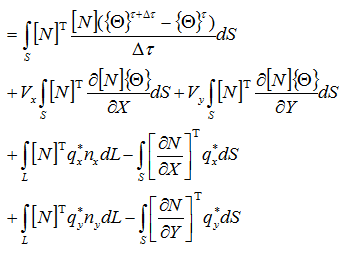
界面に作用する伝熱の項をまとめると

熱流束を展開して
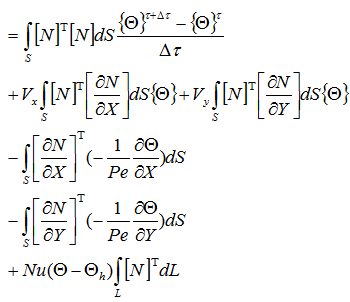
項ごとに分解して

温度を内挿関数で表示して
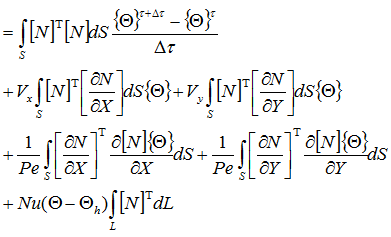
温度は定数なので積分の外に出す
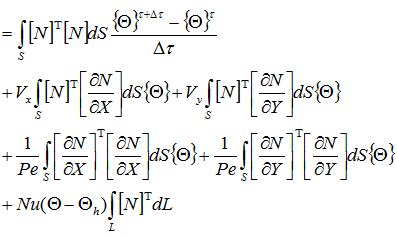
行列式で表す
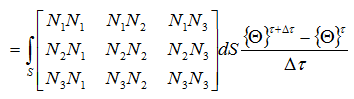
対流項
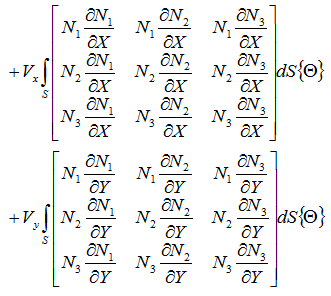
伝導伝熱の項
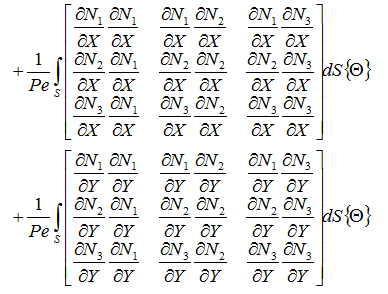
対流伝熱の項
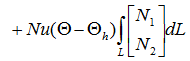
内挿関数を形状関数に直す
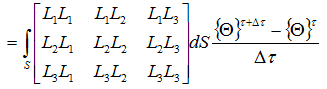
対流項
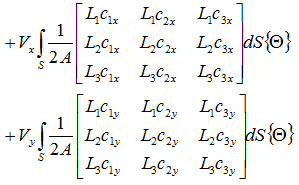
伝導伝熱の項
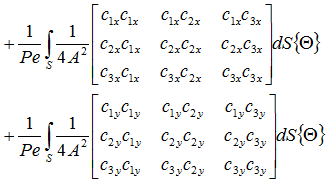
対流伝熱の項
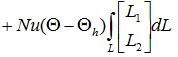
ここで、面積積分、体積積分の公式より
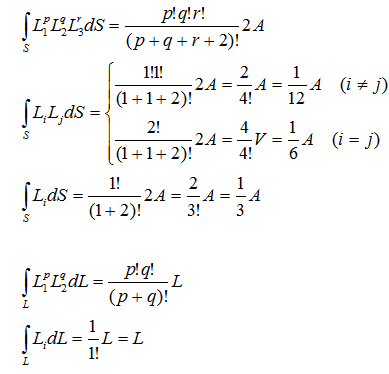
形状関数を積分すると
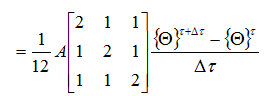
対流項
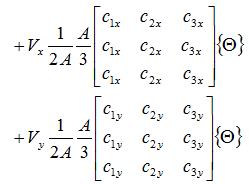
伝導伝熱の項
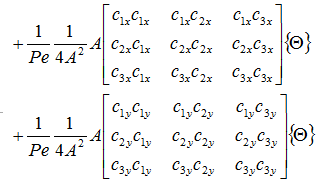
対流伝熱の項
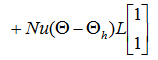
係数をまとめて
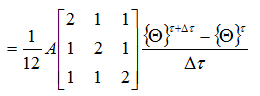
対流項
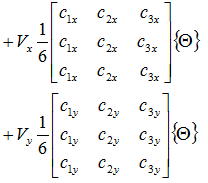
伝導伝熱の項
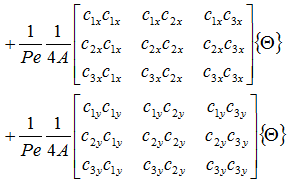
対流伝熱の項
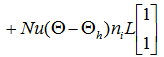
行列式をまとめると
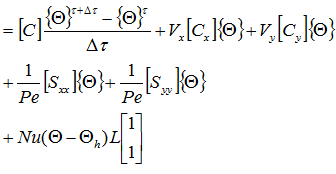
行列ごとにまとめると
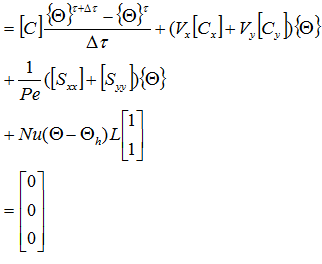
最終的に次式が導出されます。
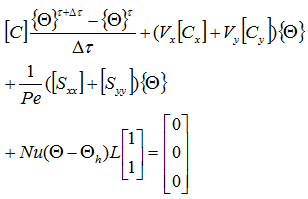
既知の項を右辺に移項します。下式は陰解法の場合の離散化式になります。
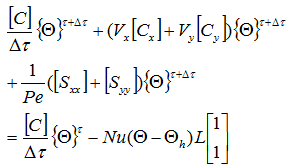
| prev | | | top | | | next |