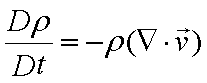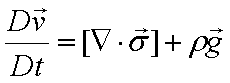広告
有限要素法
有限要素法(Finite Element Method)とは、 解析する領域を3角形や4角形などで細分化し、それら1つ1つに方程式を 当てはめて、まとめて解くことで物理量を計算する方法です。 細分化のより詳細な説明についてはこちら を参照して下さい。
数値計算の目的は、導出された支配方程式をプログラム化して、 現象をパソコンの画面上に可視化することで知見を得ることです。 有限要素法もその手法の1つです。
流体力学で導出された微分方程式はそのままではプログラム化することは できません。有限要素法では、離散化(細分化すること)という作業が 行われ、微分方程式が行列式に変換されることで、プログラムが可能になります。
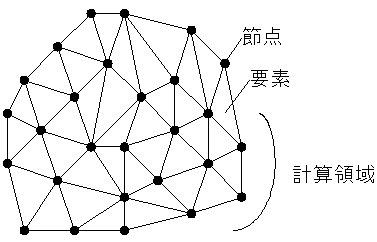
有限要素法では、節点といくつかの節点から構成される要素が用いられます。 各節点は、速度、座標などの情報を持っており、 節点の物理量から各要素の積分値が計算されます。 計算では、各要素で収支式の積分が行われます。
積分値は行列式で表されます。全要素の行列式を組み合わせ、 1つの大きな多元1次連立方程式を解くことで、 速度などの変数が計算されます。
この行列式の計算は、タイムステップごとに計算されます。 タイムステップとは、総計算時間に対するユーザーが設定する微小時間です。 つまり、時間のかかる地道な計算であり、現象は少しずつ解析されます。
計算領域は、要素全体で表されます。
| prev | | | top | | | next |