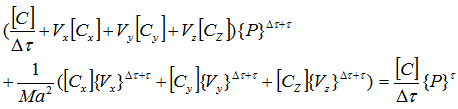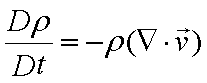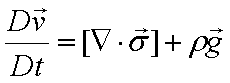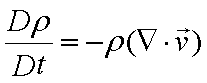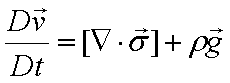広告
・質量収支式の離散化
無次元化した質量収支式は次式となります。
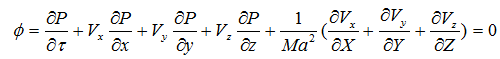
内挿関数Niを重み関数に使用すると離散化式は次式となります。
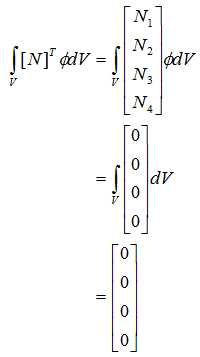
速度、圧力は、内挿関数Niを用いてそれぞれ次式で表されます。
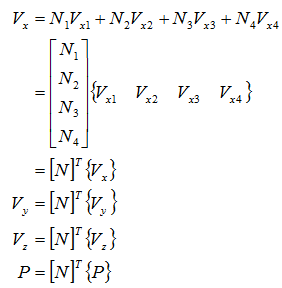
離散化式は、次式となります。

項ごとに分解して
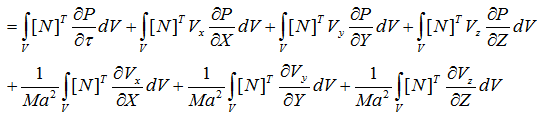
速度、圧力を内挿関数で表示して
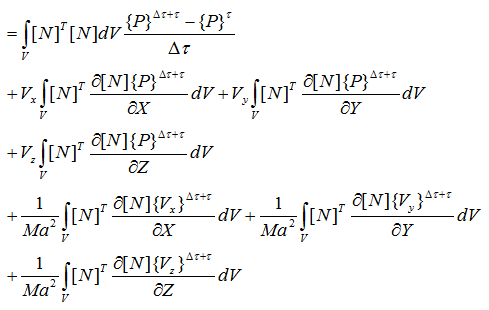
速度、圧力は定数なので積分の外に出す
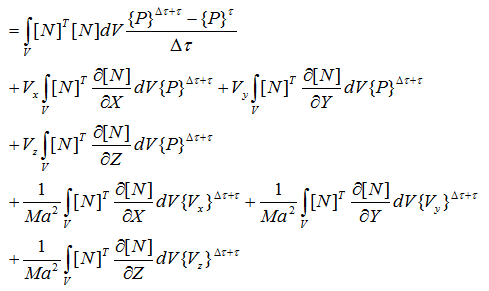
行列式で表す
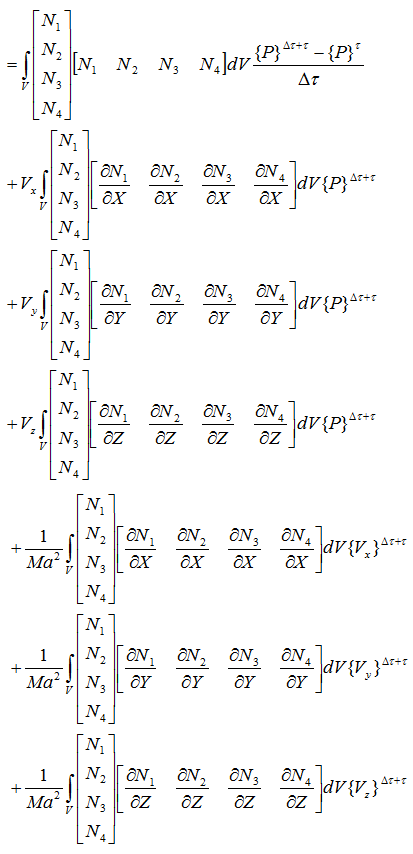
行列を計算する

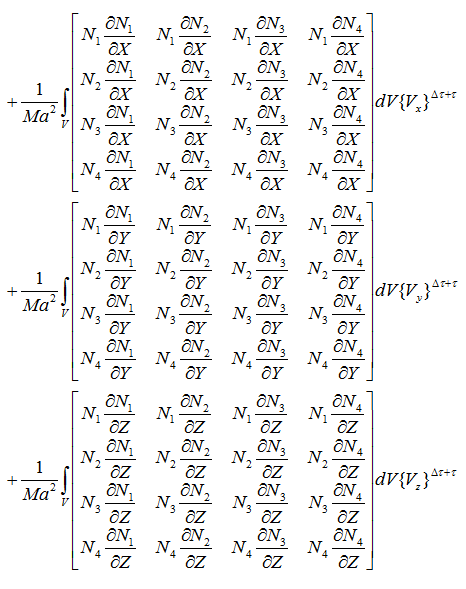
内挿関数を形状関数に直す
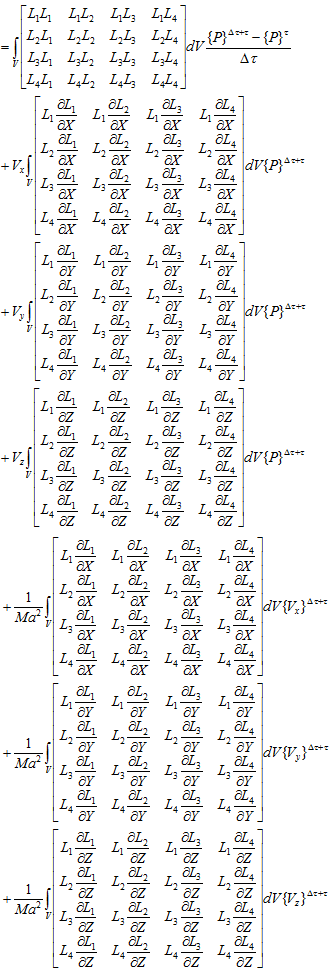
形状関数の微分値を計算する
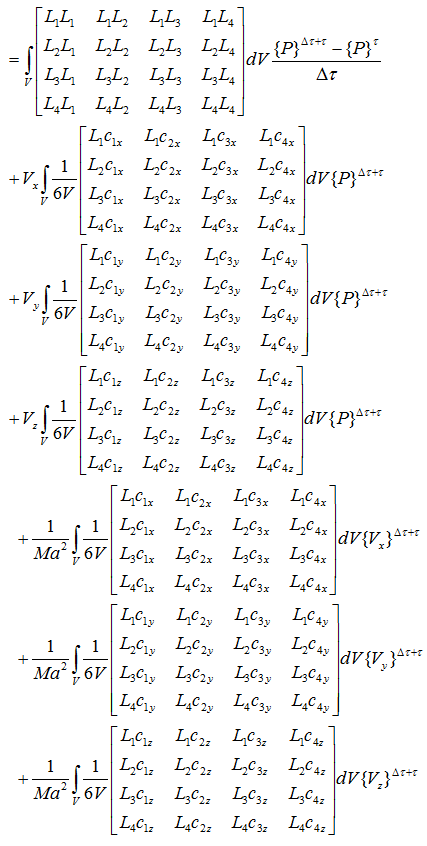
ここで、体積積分の公式より

形状関数を積分すると
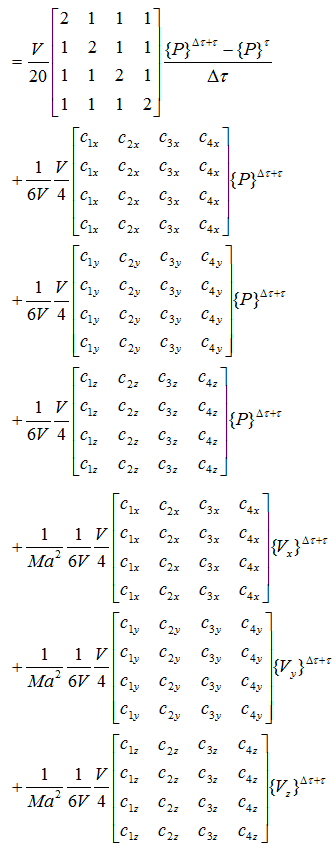
係数をまとめて
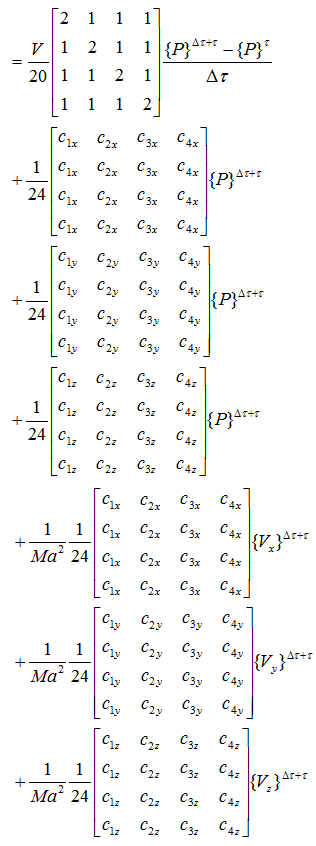
行列式をまとめると
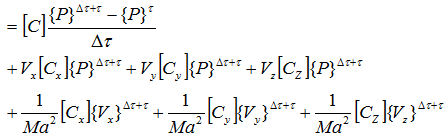
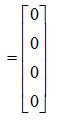
最終的に次式が導出されます。
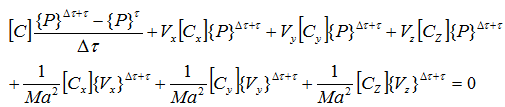
既知の項を右辺に移項します。

行列ごとにまとめると