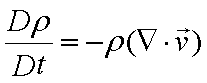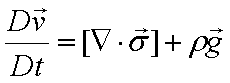広告
・運動量収支式の離散化
x, y, z軸方向の無次元化した運動量収支式は次式となります。
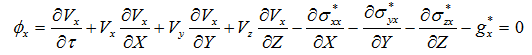
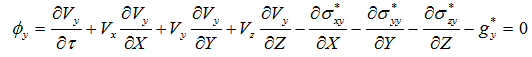
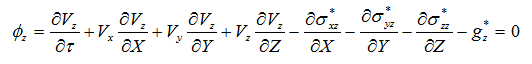
内挿関数Niを重み関数に使用すると離散化式は次式となります。
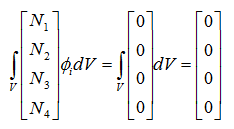
速度、圧力は、内挿関数Niを用いてそれぞれ次式で表されます。
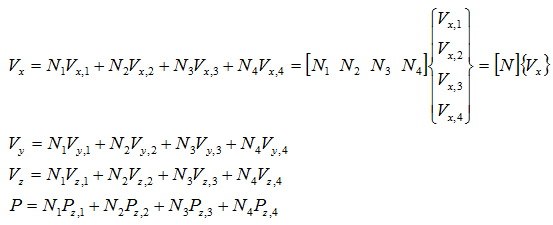
i軸方向の離散化式は、次式となります。
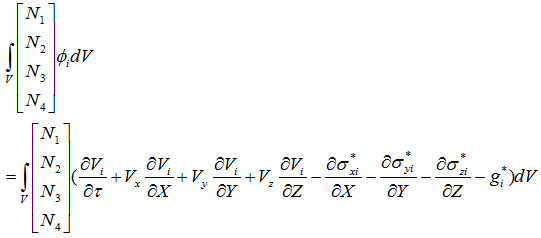
展開すると
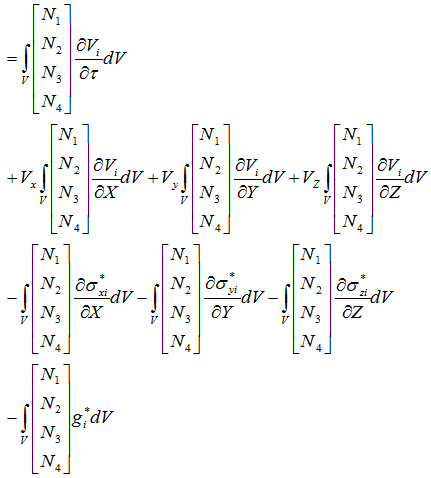
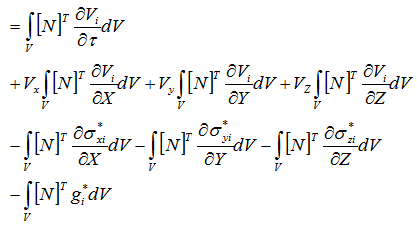
グリーン・ガウスの定理より
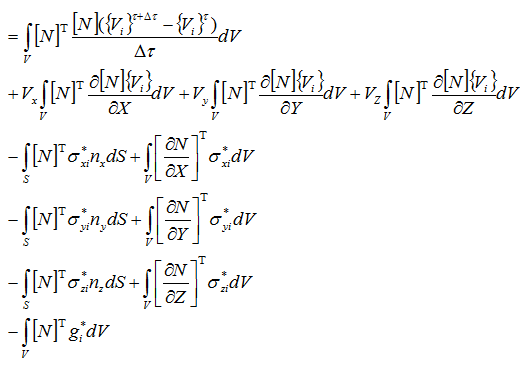
界面に作用する応力をまとめると
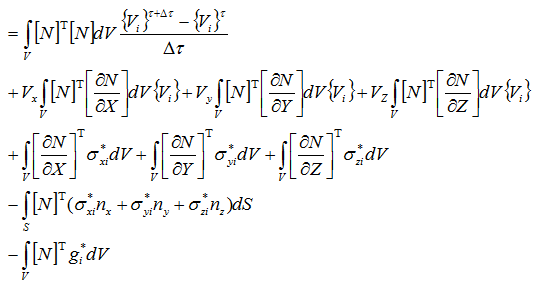
応力を展開して
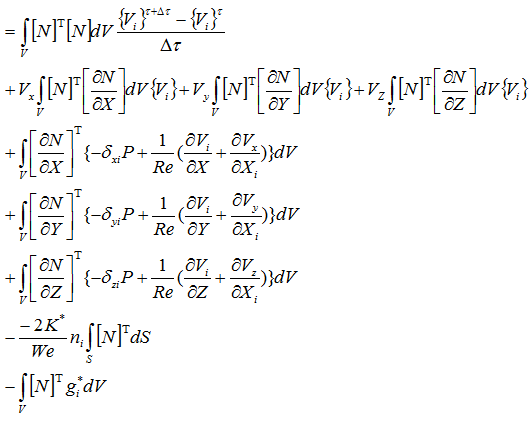
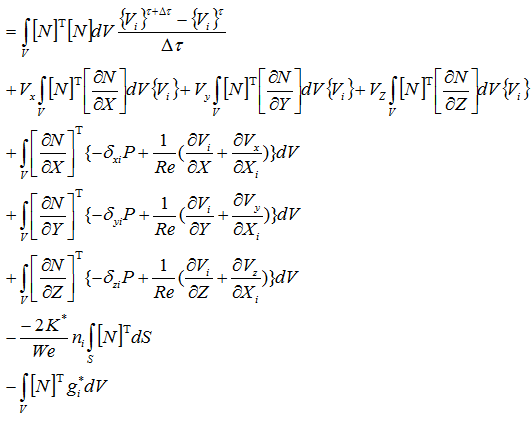
項ごとに分解して
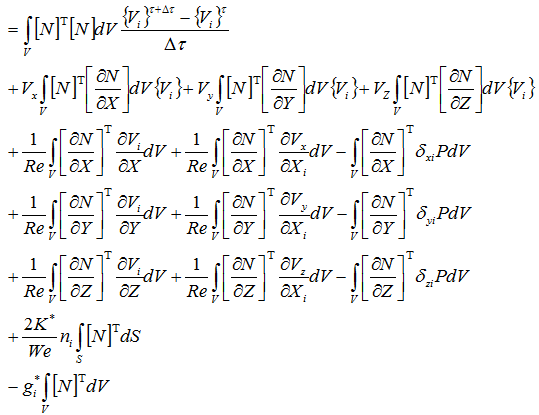
速度、圧力を内挿関数で表示して
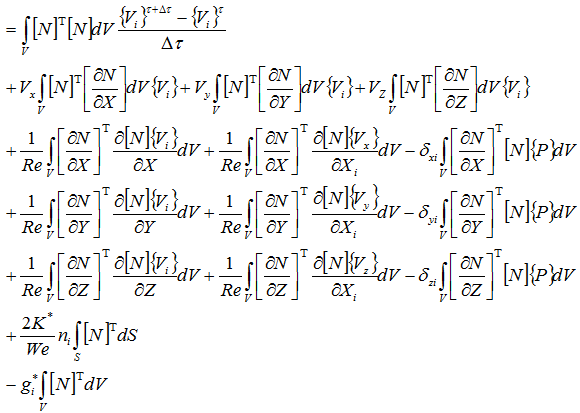
速度、圧力は定数なので積分の外に出す
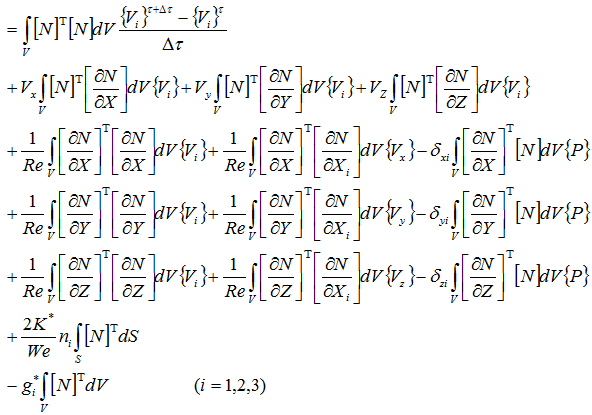
行列式で表す
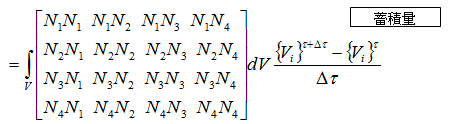
対流項
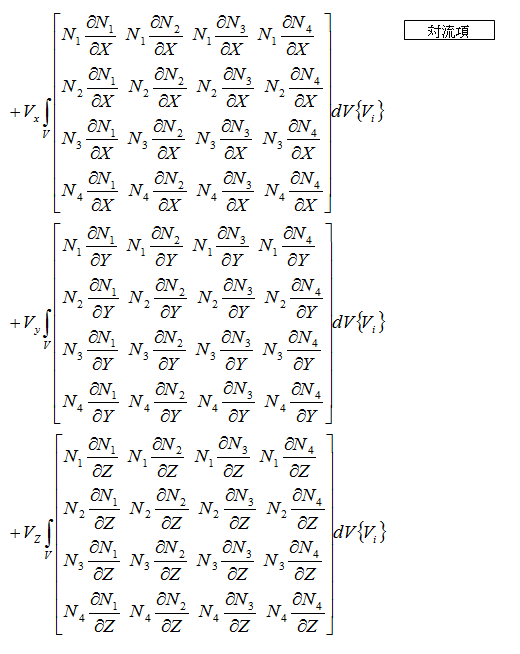
x軸方向の粘性項と圧力項

y軸方向の粘性項と圧力項

z軸方向の粘性項と圧力項

表面張力項
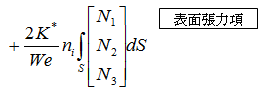
重力項
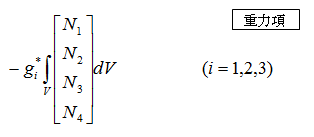
内挿関数を形状関数に直す
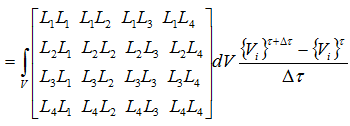
対流項
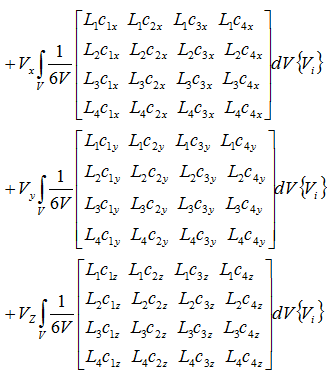
x軸方向の粘性項と圧力項
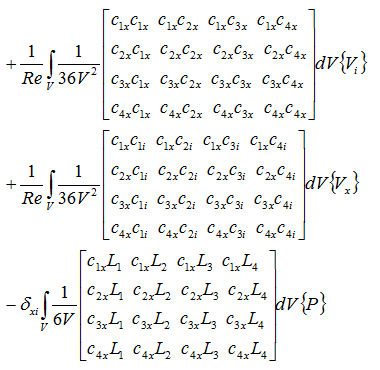
y軸方向の粘性項と圧力項
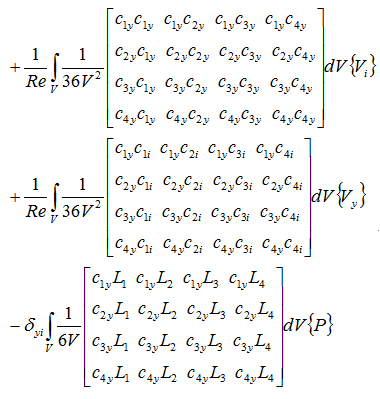
z軸方向の粘性項と圧力項
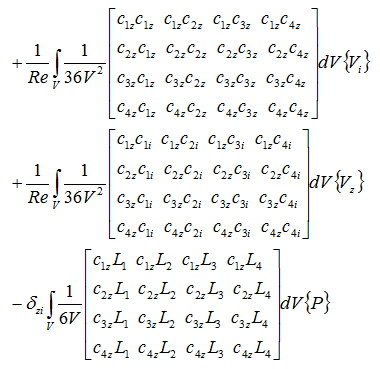
表面張力項
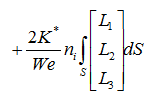
重力項
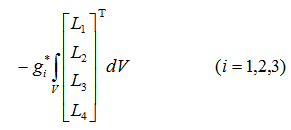
ここで、面積積分、体積積分の公式より
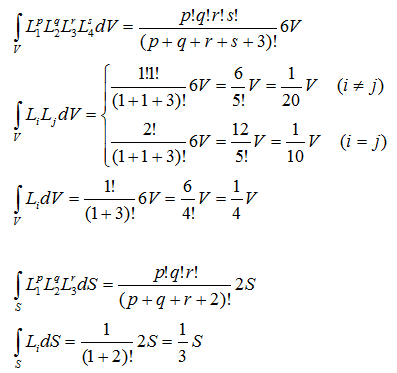
形状関数を積分すると
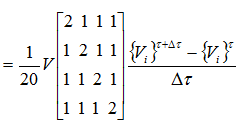
対流項
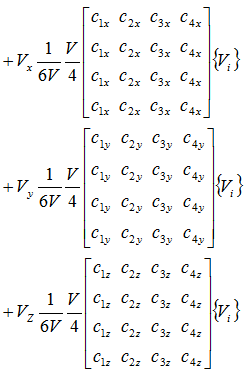
x軸方向の粘性項と圧力項
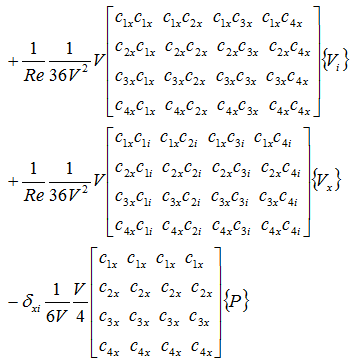
y軸方向の粘性項と圧力項
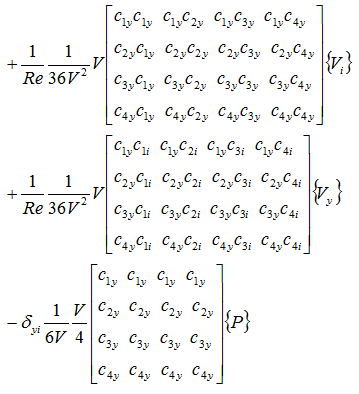
z軸方向の粘性項と圧力項

表面張力項
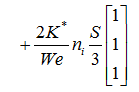
重力項
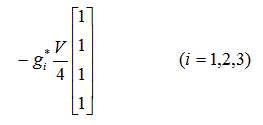
係数をまとめて
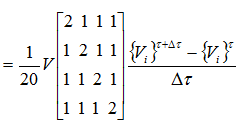
対流項
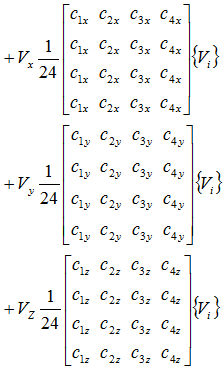
x軸方向の粘性項と圧力項
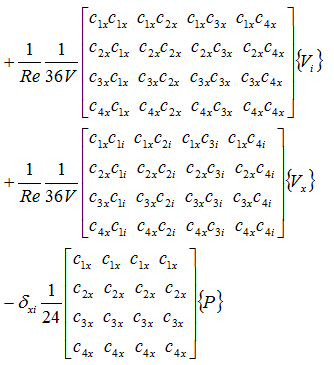
y軸方向の粘性項と圧力項
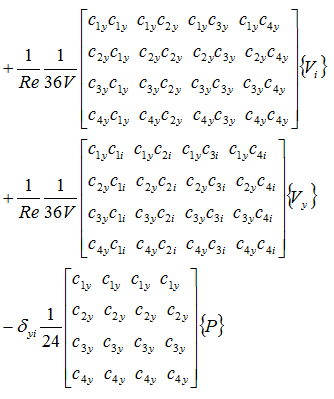
z軸方向の粘性項と圧力項
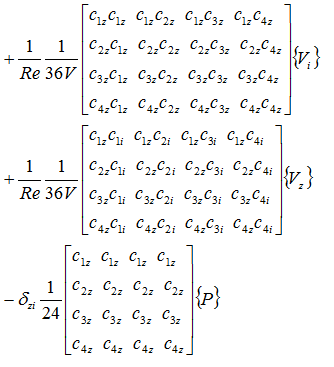
表面張力項
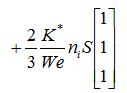
重力項
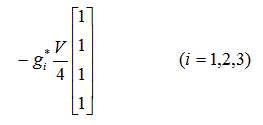
行列式をまとめると
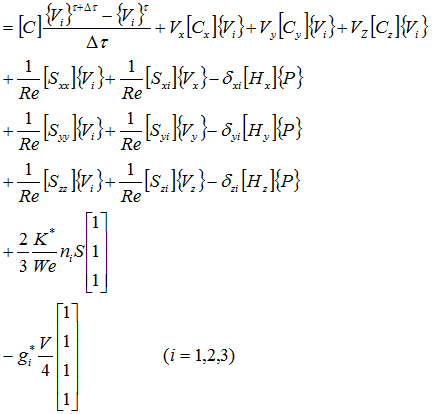
行列ごとにまとめると
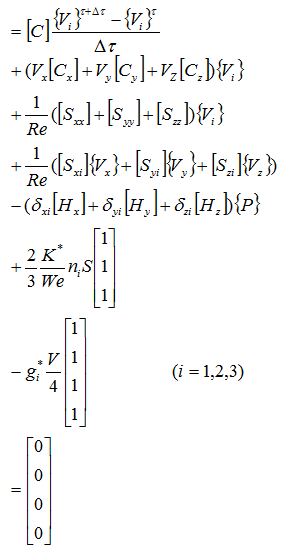
最終的に次式が導出されます。
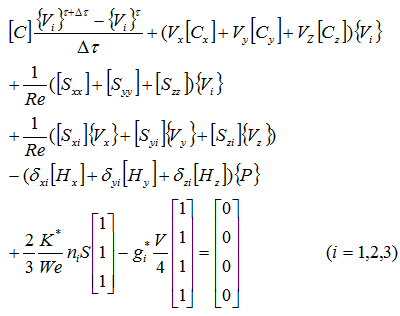
既知の項を右辺に移項します。
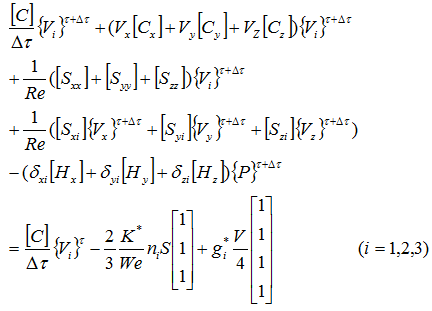
x軸方向の成分は次式となります。
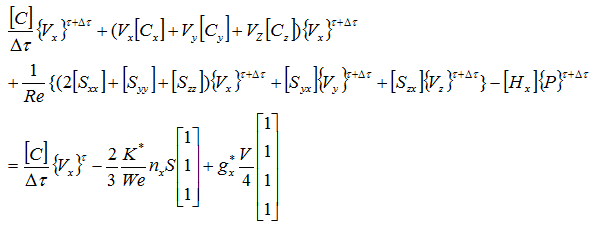
y軸方向の成分は次式となります。
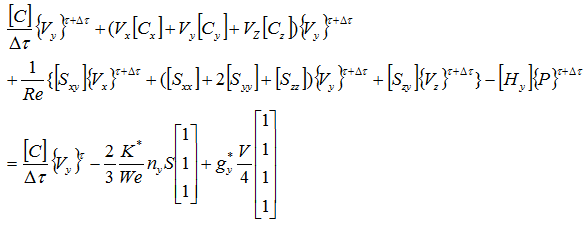
z軸方向の成分は次式となります。
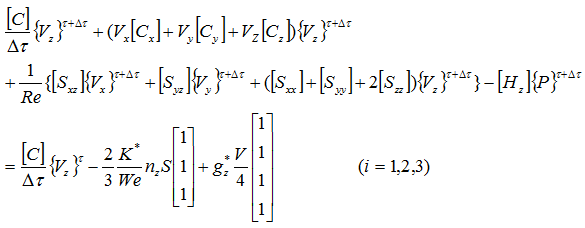
| prev | | | up | | | next |