広告
・ガウスの消去法
ガウスの消去法は、直接、連立方程式を解く方法です。
この解法で3元1次方程式を解いてみます。
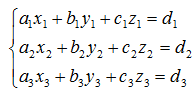
上式を行列式で表すと次式となります。
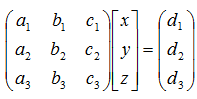
これを次式の形に直すと変数がわかります。
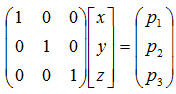
1つの行列で表すと次式となります。

手順1.
・1行目を係数a1で割る。
・2行目を係数a2で割る。
・3行目を係数a3で割る。
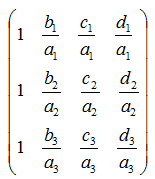
手順2.1行目を引く。
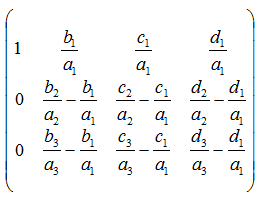
手順3.係数を次式で置き換える。

手順4.
・2行目を係数s1で割る。
・3行目を係数t1で割る。

手順5.2行目を引く。
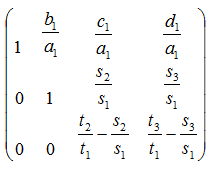
連列方程式に直すと次式となります。 z→ y→ xの順番に変数が計算できます。
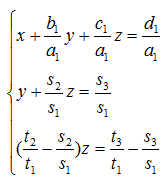
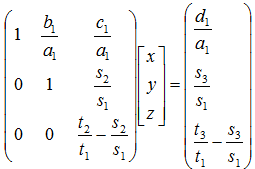
・ポイント
割り算をする係数が0の場合は、計算ができません。 係数が0となる場合は、列を入れ替える必要があります。 割り算をする係数は、aii成分です。
| prev | | | up | | | next |