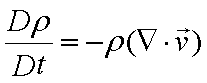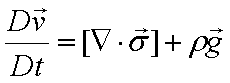広告
お知らせ等
2016.5.20 図式の解像度を向上。
2016.5.22 動画追加(無次元数)
数値計算について
流体力学や有限要素法、数値計算 についてわかり易く説明している(つもり)サイトです。 有限要素法は数値計算を行うための強力な手法の1つです。 しかし、理解するためには高校で習う物理から流体力学、プログラミング、メッシュ作成などの 幅広い知識が必要になります。それらの内容を学ぶ順番に下記に示してみます。
・古典力学
基本となる知識は、古典力学です。 質量[kg]、長さ[m]、時間[s]などの SI単位の意味や 速度[m/s]、運動量[N・s]、エネルギー[N・m]などの 物理量の意味について考えます。 使用する数学は、基本的なベクトルや微分積分などです。
・流体力学
古典力学の次に学ぶのは、流体力学です。 流体力学とは、水や空気などの流体 が流れる現象を力学的に解析する学問です。流体にはどの様な力が作用するかを考えて、それらの作用する力、 慣性力 、せん断応力 、圧力 、重力などを具体的に式で表すことから始まります。 そしてそれらの力の収支を取ると収支式が導出されます。 質量の収支式は連続の式 、そして運動量の収支式はナヴィエ・ストークスの式 と呼ばれています。これらの収支式は、数値計算を行うための重要な基礎式になります。 流体力学を学ぶには内積や 外積、面積分や体積分などの知識が必要になります。
・有限要素法
有限要素法(Finite Element Method:FEM)は、 流体力学で導出された連続の式やナヴィエ・ストークスなどの微分方程式を 離散化 という作業で行列式に分解する方法です。この離散化によって微分方程式を四則演算のプログラム で記述することが可能になります。有限要素法には 節点や要素 、また形状関数 や内挿関数といった考え方が出てきます。 また、解析領域の界面 を扱うためにグリーン・ガウスの定理 やラプラスの式といった公式を使用します。
・数値計算
数値計算は方程式をプログラミングするための手法です。離散化された式を解く際には、 膨大な連立方程式を解く方法が必要になります。これには ガウスの消去法などが利用されます。 また、 自由表面を扱う際には 最小二乗法という考えが必要になる場合があります。 また、ヤコビアン行列という座標変換に必要な行列ついて学ぶ必要もあります。 テーラー展開の考えも必要になります。特に有限要素法の場合は、 バンド幅の最適化が重要になります。
・プログラミング
プログラミングにはフォートラン (fortran)などが使われています。それほど難しい言語ではありません。 変数や 配列の宣言、 関数の定義などが理解できれば 基本的には十分だと思います。フォートランの特徴は、変数の頭文字でその変数の型が決まることでしょうか。 また、左側をラベル用に7文字分空けることも大きな特徴の1つです。
・メッシュ作成
数値解析を行う上で、メッシュ の作成はとても重要です。有限要素法で数値解析を行うためには、 解析領域を3角形 や4面体 などの集まりに変換する必要があります。このメッシュ作成の手法として デローニ分割 などがあり、解析領域が複雑な場合ほどメッシュ作成も困難になります。 特に水などの自由表面を扱う場合などは要素の変形 が大きいため解析は大変です。また、精度の良い計算を行うためには、 より滑らかな節点配置を行う必要があります。
・上記以外
ここに述べた以外にも乱流や粘弾性流体、構造物との連成解析など、数値計算は幅広く利用されています。 また、有限要素法に限らず、差分法や有限体積法、粒子法など様々な解析方法が存在します。
動画
バブルメッシュ法(bubble mesh method) 詳しくは こちら
こちら
デローニ分割後

デローニ分割(delaunay method) 詳しくは こちら
こちら
レイノルズ数 詳しくは こちら
こちら
ウェーバー数 詳しくは こちら
こちら
メインコンテンツ
サイト内検索