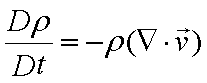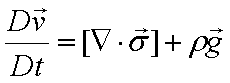広告
サイトマップ
物理
- SI単位
- 物理量
- 単位ベクトル
- 物理量の分類
- 作用素の種類
- 計算の種類
- 四則演算
- 内積
- クロネッカーのデルタ
- (ベクトル・ベクトル)
- (∇・ベクトル) 発散
- (∇・テンソル)
- ラプラシアン
- 全微分作用素
- 内積からの角度計算
- 外積
- 準備
- [ベクトル×ベクトル]
- [∇×ベクトル]
- 公式
- オーダー一覧
流体力学
- 流体
- 流体の物性
- 使用する収支式
- 質量収支式
- 粘性力の簡単な説明
- 力の種類
- 慣性力
- 粘性力
- 圧力
- 重力
- 収支式の導出
- 運動量収支式
- 応力の詳細
- せん断速度
- 垂直成分
- 圧力について
- 剪断成分の対称性
- 剪断成分の値
- 応力のまとめ
- 境界に作用する力
- 表面張力
- 壁面の速度
- 蒸発
- 無次元数
- レイノルズ数
- ウェーバー数
- オーネソルジュ数
- ボンド数
- フルード数
- マッハ数
- 無次元化
- 質量収支式
- 運動量収支式
- 代表速度、代表長さ
- グリーン・ガウスの定理
有限要素法
- 節点・要素
- 形状関数・内挿関数
- 3角形1次要素
- 3角形2次要素
- 4面体1次要素
- 要素の積分
- 3角形要素の面積
- 4面体要素の体積
- 内挿関数の微分
- 3角形1次要素
- 要素の面積
- 内挿関数N1の微分
- 内挿関数N2の微分
- 内挿関数N3の微分
- まとめ
- 4面体1次要素
- 要素の体積
- 内挿関数N1の微分
- 内挿関数N2の微分
- 内挿関数N3の微分
- 内挿関数N4の微分
- まとめ
- 離散化
- 3角形1次要素
- 質量収支式
- 運動量収支式
- 4面体1次要素
- 質量収支式
- 運動量収支式
- 境界条件
- 第1種
- 第2種
- 表面張力
- 勾配0
- 第3種
- 座標の取り方
- マトリックス作成
- 行列計算
- ガウスの消去法
- コレスキー解
- バンド幅の最適化
- バンド幅の最適化方法
メッシュ
SIMPLE法
Appendix
コラム
伝熱工学
fortran
- コメント
- 変数の型宣言
- 配列宣言
- parameter文
- data文
- function関数
- subroutine関数
- common文
- include文
- do文
- if文
- cycle、exit文
- ファイル操作
- goto文
| prev | | | top | | | next |